La taula següent mostra les característiques dels materials de quatre provetes normalitzades que s’utilitzen en un assaig de tracció. (Totes les provetes tenen les mateixes dimensions.)
| \(Densitat\) \((kg/(m^3)\) | \(Mòdul\) \(d’elasticitat\) \((GPa)\) | \(Límit\) \(elàstic\) \((MPa)\) | \(Tensió\) \(de\) \(ruptura\) \((MPa)\) | |
|---|---|---|---|---|
| Alumini pur | 2 710 | 69 | 85 | 100 |
| Molibdè pur | 10 220 | 324 | 565 | 655 |
| Níquel | 8 900 | 207 | 138 | 483 |
| Plata | 10 490 | 76 | 55 | 125 |
Es pot afirmar que, per a un mateix esforç de tracció, la proveta que menys es deformarà és la que està feta
Amb quines unitats es pot expressar l’energia elèctrica consumida en una llar?
En un circuit elèctric, es connecten en sèrie dues resistències de valors nominals 110 Ω i 330 Ω i tolerància ±5 %. Es pot afirmar que
Quina potència necessita una cafetera per a escalfar 75 mL d’aigua que es troba a temperatura ambient \((T_{a} = 21 °C)\) fins a 88 °C en 20 s? La calor específica de l’aigua és \(c_{e} = 4,187 J/(g · K)\).
Una terrassa d’un bar té instaŀlades 5 estufes de gas butà que funcionen durant 9 h al dia i cadascuna d’elles consumeix 800 g/h de butà. L’Oficina Catalana del Canvi Climàtic estima un factor d’emissió FE = 2,96 kg de \(CO_{2}\) per cada kilogram de gas butà. Quina és la petjada de carboni que deixen les 5 estufes al cap d’un dia de funcionament?
Un sistema digital té l’esquema de portes lògiques següent:
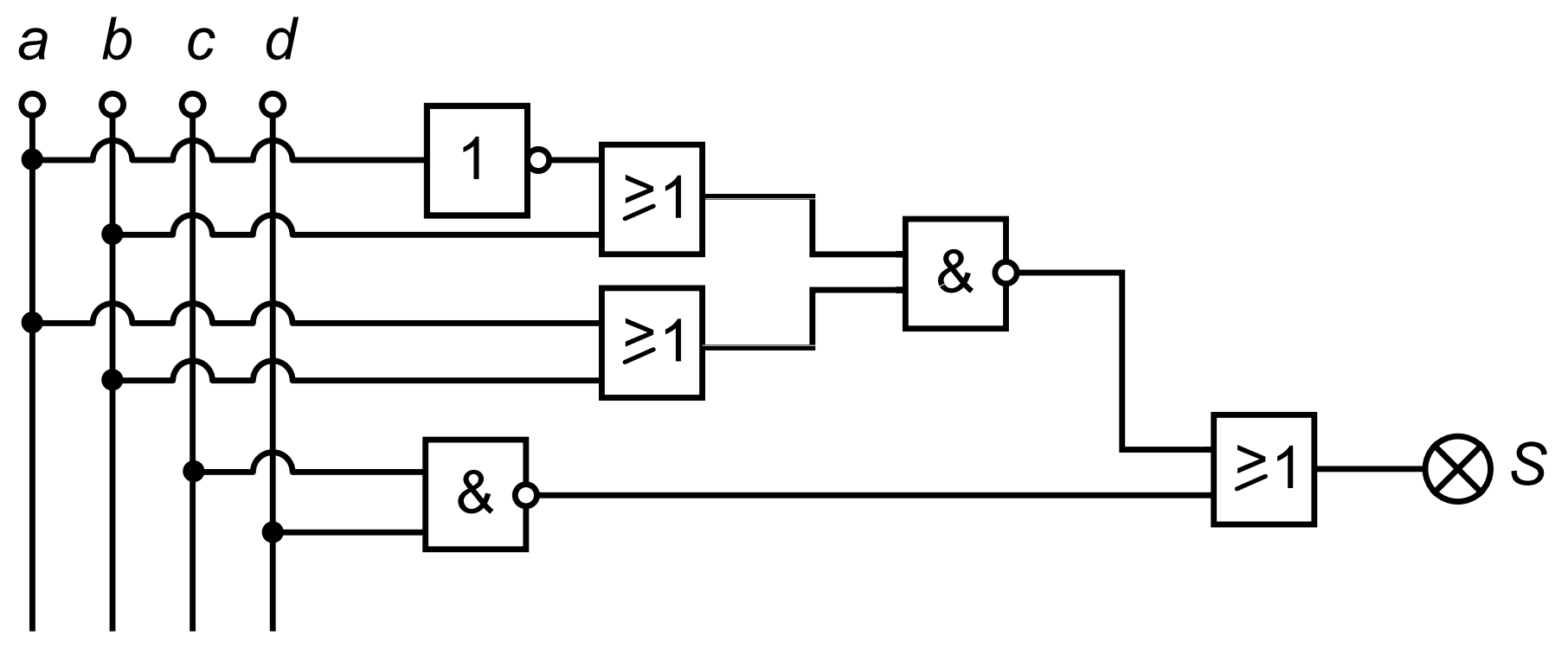
a) Determineu la funció lògica entre les variables a, b, c, d i S.
Si escau, simplifiqueu-la.
b) Elaboreu la taula de veritat del sistema.
c) Dibuixeu l’esquema de contactes de la funció simplificada.
Un muntacàrregues és accionat per un motor reductor de rendiment η = 0,6. El motor d’inducció monofàsic es connecta a una tensió U = 230 V i funciona amb un factor de potència cos φ = 0,85. La relació de transmissió del reductor és τ = \(ω_{red}\)/\(ω_{mot}\) = 0,009. El motor gira a \(n_{mot}\) = 1470 \(min^{–1}\) i l’aparell eleva h = 8 m una càrrega de massa m = 2000 kg en t = 1,5 min a una velocitat constant. Determineu:
a) La velocitat de rotació de l’eix de sortida del reductor \(ω_{red}\) en rad/s.
Inserta els valors:
b) El treball necessari que ha de realitzar el muntacàrregues W.
Inserta els valors:
c) La potència elèctrica consumida pel conjunt \(P_{elèc}\).
Inserta els valors:
d) La intensitat de corrent I.
Inserta els valors:
Un automòbil està equipat amb un motor de \(n_{c}\) = 6 cilindres de cursa s = 91 mm i diàmetre d = 83 mm. La relació de compressió és rc = 12. Quan l’automòbil es desplaça per un terreny horitzontal a una velocitat constant, el motor desenvolupa una potència \(P_{mec}\) = 20 kW, gira a n = 3 000 \(min^{-1}\) i consumeix c = 6,5 L/h de benzina de poder calorífic \(p_{c}\) = 42 000 kJ/kg i densitat ρ = 0,8 kg/L. Determineu:
a) La cilindrada total V en \(cm^{3}\).
Inserta els valors:
b) El parell Γ que subministra el motor.
Inserta els valors:
c) La potència tèrmica consumida \(P_{tèrm}\) expressada en kW.
Inserta els valors:
d) El rendiment del motor η.
Inserta els valors:
La figura representa el sistema que permet elevar el taulell d’una taula de centre. El taulell és homogeni i de gruix negligible. Té una longitud 3L i una massa m = 4 kg. Les barres AB i CD, de massa negligible, tenen els extrems articulats al taulell i a l’estructura de la taula, que està fixada al terra. S’aplica una força F vertical al punt O.
a) Dibuixeu el diagrama de cos lliure del taulell.
b) El valor de la força F aplicada.
Inserta els valors:
c) El valor de les forces \(F_{AB}\) i \(F_{CD}\) que fan les barres sobre el taulell. Treballen a compressió o a tracció?
Inserta els valors:
S’instaŀlen n = 7 estufes elèctriques de potència \(P_{1}\) = 900 W a la terrassa d’un bar i s’alimenten a una tensió \(U{1}\) = 230 V. Determineu:
a) El corrent \(I_{i}\) que circula per cada estufa i el corrent total \(I\).
Inserta els valors:
b) El valor de la resistència elèctrica de cada estufa R.
Inserta els valors:
c) La potència \(P_{2}\) que consumiria cada estufa si s’alimentés a una tensió \(U_{2}\) = 125 V.
Inserta els valors: